what does it mean to say that mass is conserved during a physical change

Scientific law that a closed system'southward mass remains abiding

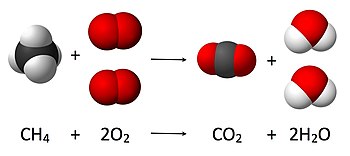
Combustion reaction of marsh gas. Where 4 atoms of hydrogen, 4 atoms of oxygen, and 1 of carbon are present before and later the reaction. The full mass after the reaction is the aforementioned as before the reaction.

In physics and chemistry, the constabulary of conservation of mass or principle of mass conservation states that for any arrangement closed to all transfers of thing and energy, the mass of the organization must remain abiding over time, as the system'south mass cannot modify, so quantity tin can neither be added nor exist removed. Therefore, the quantity of mass is conserved over time.

The law implies that mass can neither be created nor destroyed, although information technology may exist rearranged in space, or the entities associated with it may be changed in grade. For case, in chemic reactions, the mass of the chemical components before the reaction is equal to the mass of the components afterwards the reaction. Thus, during any chemical reaction and low-energy thermodynamic processes in an isolated organisation, the total mass of the reactants, or starting materials, must be equal to the mass of the products.

The concept of mass conservation is widely used in many fields such as chemistry, mechanics, and fluid dynamics. Historically, mass conservation in chemical reactions was demonstrated independently past Mikhail Lomonosov and later rediscovered past Antoine Lavoisier in the late 18th century. The formulation of this law was of crucial importance in the progress from alchemy to the modern natural scientific discipline of chemistry.

In reality, the conservation of mass only holds approximately and is considered part of a series of assumptions in classical mechanics. The law has to be modified to comply with the laws of quantum mechanics and special relativity nether the principle of mass-energy equivalence, which states that energy and mass grade one conserved quantity. For very energetic systems the conservation of mass-simply is shown not to hold, as is the case in nuclear reactions and particle-antiparticle annihilation in particle physics.

Mass is also non generally conserved in open systems. Such is the case when various forms of energy and thing are immune into, or out of, the organisation. However, unless radioactivity or nuclear reactions are involved, the corporeality of energy escaping (or entering) such systems every bit heat, mechanical work, or electromagnetic radiation is ordinarily too small to be measured as a decrease (or increase) in the mass of the system.

For systems which include big gravitational fields, general relativity has to exist taken into account; thus mass-energy conservation becomes a more than complex concept, subject to different definitions, and neither mass nor free energy is every bit strictly and simply conserved equally is the instance in special relativity.

Formulation and examples [edit]

The law of conservation of mass can only be formulated in classical mechanics, in which the energy scales associated to an isolated system are much smaller than ${\displaystyle mc^{two}}$ , where ${\displaystyle m}$ is the mass of a typical object in the organisation, measured in the frame of reference where the object is at residuum, and ${\displaystyle c}$ is the speed of low-cal.

The police can be formulated mathematically in the fields of fluid mechanics and continuum mechanics, where the conservation of mass is usually expressed using the continuity equation, given in differential grade equally

${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {v} )=0,}$

where ${\textstyle \rho }$ is the density (mass per unit volume), ${\textstyle t}$ is the fourth dimension, ${\textstyle \nabla \cdot }$ is the departure, and ${\textstyle \mathbf {v} }$ is the catamenia velocity field. The interpretation of the continuity equation for mass is the post-obit: For a given closed surface in the organisation, the change, over whatsoever fourth dimension interval, of the mass enclosed by the surface is equal to the mass that traverses the surface during that time interval: positive if matter goes in and negative if affair goes out. For the whole isolated system, this status implies that the total mass ${\textstyle G}$ , the sum of the masses of all components in the organization, does not change over time, i.eastward.

${\displaystyle {\frac {{\text{d}}Yard}{{\text{d}}t}}={\frac {\text{d}}{{\text{d}}t}}\int \rho {\text{d}}V=0}$ ,

where ${\textstyle {\text{d}}V}$ is the differential that defines the integral over the whole volume of the system.

The continuity equation for the mass is role of Euler equations of fluid dynamics. Many other convection–improvidence equations describe the conservation and menstruum of mass and matter in a given arrangement.

In chemistry, the calculation of the amount of reactant and products in a chemical reaction, or stoichiometry, is founded on the principle of conservation of mass. The principle implies that during a chemical reaction the total mass of the reactants is equal to the full mass of the products. For case, in the following reaction

CH
_iv + iiO
₂ → CO
₂ + 2H
₂ O,

where ane molecule of methane (CH
_four ) and ii oxygen molecules O
_two are converted into one molecule of carbon dioxide (CO
₂ ) and two of water (H
₂ O). The number of molecules resulting from the reaction can exist derived from the principle of conservation of mass, as initially 4 hydrogen atoms, iv oxygen atoms and one carbon atom are present (as well as in the final land); thus the number water molecules produced must be exactly ii per molecule of carbon dioxide produced.

Many engineering science problems are solved by following the mass distribution of a given organization over time; this methodology is known as mass balance.

History [edit]

Every bit early as 520 BCE, Jain philosophy, a non-creationist philosophy based on the teachings of Mahavira,^[4] stated that the universe and its constituents such every bit matter cannot be destroyed or created. The Jain text Tattvarthasutra (2nd century CE) states that a substance is permanent, merely its modes are characterised by creation and devastation.^[5]

An important thought in ancient Greek philosophy was that "Nil comes from nothing", and so that what exists now has always existed: no new matter can come into existence where in that location was none earlier. An explicit statement of this, along with the further principle that cipher tin can laissez passer abroad into nothing, is found in Empedocles (c.4th century BCE): "For it is impossible for anything to come to exist from what is non, and it cannot be brought about or heard of that what is should exist utterly destroyed."^[6]

A further principle of conservation was stated past Epicurus around the tertiary century BCE, who wrote in describing the nature of the Universe that "the totality of things was e'er such as it is at present, and always will be".^[7]

Discoveries in chemistry [edit]

By the 18th century the principle of conservation of mass during chemic reactions was widely used and was an of import assumption during experiments, even before a definition was formally established,^[eight] equally can exist seen in the works of Joseph Black, Henry Cavendish, and Jean Rey.^[9] The first to outline the principle was Mikhail Lomonosov in 1756. He may have demonstrated it past experiments and certainly had discussed the principle in 1748 in correspondence with Leonhard Euler,^[10] though his merits on the subject is sometimes challenged.^{[11] [12]} According to the Soviet physicist Yakov Dorfman:

The universal law was formulated past Lomonosov on the ground of general philosophical materialistic considerations, it was never questioned or tested by him, simply on the contrary, served him equally a solid starting position in all research throughout his life. ^[thirteen]

A more refined series of experiments were afterward carried out by Antoine Lavoisier who expressed his determination in 1773 and popularized the principle of conservation of mass. The demonstrations of the principle disproved the then pop phlogiston theory that said that mass could be gained or lost in combustion and heat processes.

The conservation of mass was obscure for millennia because of the buoyancy effect of the World's atmosphere on the weight of gases. For example, a piece of wood weighs less subsequently called-for; this seemed to suggest that some of its mass disappears, or is transformed or lost. This was not disproved until careful experiments were performed in which chemical reactions such as rusting were allowed to take place in sealed glass ampoules; information technology was found that the chemical reaction did non alter the weight of the sealed container and its contents. Weighing of gases using scales was not possible until the invention of the vacuum pump in the 17th century.

Once understood, the conservation of mass was of great importance in progressing from alchemy to modern chemistry. Once early chemists realized that chemical substances never disappeared but were merely transformed into other substances with the same weight, these scientists could for the first fourth dimension embark on quantitative studies of the transformations of substances. The idea of mass conservation plus a surmise that certain "elemental substances" also could non be transformed into others by chemic reactions, in plow led to an understanding of chemic elements, as well every bit the thought that all chemic processes and transformations (such as burning and metabolic reactions) are reactions between invariant amounts or weights of these chemic elements.

Following the pioneering work of Lavoisier, the exhaustive experiments of Jean Stas supported the consistency of this police force in chemical reactions,^[14] fifty-fifty though they were carried out with other intentions. His inquiry^{[fifteen] [xvi]} indicated that in certain reactions the loss or gain could not accept been more than 2 to four parts in 100,000.^[17] The difference in the accuracy aimed at and attained by Lavoisier on the one manus, and by Morley and Stas on the other, is enormous.^[18]

Modern physics [edit]

The police force of conservation of mass was challenged with the appearance of special relativity. In one of the Annus Mirabilis papers of Albert Einstein in 1905, he suggested an equivalence betwixt mass and energy. This theory implied several assertions, similar the idea that internal energy of a organisation could contribute to the mass of the whole organisation, or that mass could be converted into electromagnetic radiation. Withal, as Max Planck pointed out, a change in mass every bit a result of extraction or addition of chemical energy, every bit predicted by Einstein'south theory, is so small that it could not exist measured with the available instruments and could not be presented equally a test of special relativity. Einstein speculated that the energies associated with newly discovered radioactivity were significant enough, compared with the mass of systems producing them, to enable their change of mass to be measured, one time the energy of the reaction had been removed from the system. This later indeed proved to be possible, although information technology was eventually to be the first artificial nuclear transmutation reaction in 1932, demonstrated by Cockcroft and Walton, that proved the starting time successful test of Einstein'south theory regarding mass loss with energy gain.

The law of conservation of mass and the analogous law of conservation of energy were finally overruled by a more than general principle known equally the mass–energy equivalence. Special relativity likewise redefines the concept of mass and energy, which tin can be used interchangeably and are defined relative to the frame of reference. Several quantities had to be defined for consistency, such every bit the residue mass of a particle (mass in the rest frame of the particle) and the relativistic mass (in another frame). The latter term is usually less frequently used.

Generalization [edit]

This article or section may incorporate misleading parts. Delight assist analyze this article according to any suggestions provided on the talk page. (December 2017)

Special relativity [edit]

In special relativity, the conservation of mass does non apply if the arrangement is open and free energy escapes. Nevertheless, it does proceed to apply to totally closed (isolated) systems. If free energy cannot escape a organisation, its mass cannot decrease. In relativity theory, and so long every bit any blazon of energy is retained within a system, this free energy exhibits mass.

Also, mass must be differentiated from affair, since matter may not be perfectly conserved in isolated systems, fifty-fifty though mass is always conserved in such systems. However, matter is then nearly conserved in chemistry that violations of thing conservation were not measured until the nuclear age, and the supposition of matter conservation remains an of import applied concept in nigh systems in chemistry and other studies that practise not involve the high energies typical of radioactivity and nuclear reactions.

The mass associated with chemic amounts of free energy is too modest to measure [edit]

The modify in mass of certain kinds of open systems where atoms or massive particles are not allowed to escape, just other types of free energy (such equally lite or oestrus) are allowed to enter, escape or be merged, went unnoticed during the 19th century, because the change in mass associated with addition or loss of pocket-sized quantities of thermal or radiant energy in chemic reactions is very modest. (In theory, mass would not change at all for experiments conducted in isolated systems where rut and work were not allowed in or out.)

Mass conservation remains correct if energy is not lost [edit]

The conservation of relativistic mass implies the viewpoint of a single observer (or the view from a unmarried inertial frame) since changing inertial frames may result in a change of the total energy (relativistic energy) for systems, and this quantity determines the relativistic mass.

The principle that the mass of a system of particles must be equal to the sum of their balance masses, even though truthful in classical physics, may be simulated in special relativity. The reason that rest masses cannot be simply added is that this does not take into account other forms of energy, such as kinetic and potential energy, and massless particles such as photons, all of which may (or may non) bear on the total mass of systems.

For moving massive particles in a organisation, examining the rest masses of the various particles also amounts to introducing many different inertial ascertainment frames (which is prohibited if total system energy and momentum are to exist conserved), and also when in the rest frame of ane particle, this procedure ignores the momenta of other particles, which touch the organization mass if the other particles are in motion in this frame.

For the special type of mass called invariant mass, changing the inertial frame of observation for a whole airtight system has no effect on the measure of invariant mass of the organization, which remains both conserved and invariant (unchanging), fifty-fifty for dissimilar observers who view the entire organisation. Invariant mass is a system combination of energy and momentum, which is invariant for any observer, because in any inertial frame, the energies and momenta of the various particles always add to the aforementioned quantity (the momentum may be negative, so the addition amounts to a subtraction). The invariant mass is the relativistic mass of the system when viewed in the center of momentum frame. It is the minimum mass which a system may exhibit, as viewed from all possible inertial frames.

The conservation of both relativistic and invariant mass applies fifty-fifty to systems of particles created past pair production, where energy for new particles may come from kinetic energy of other particles, or from 1 or more than photons as part of a system that includes other particles besides a photon. Again, neither the relativistic nor the invariant mass of totally closed (that is, isolated) systems changes when new particles are created. Even so, different inertial observers will disagree on the value of this conserved mass, if it is the relativistic mass (i.e., relativistic mass is conserved but non invariant). Yet, all observers agree on the value of the conserved mass if the mass beingness measured is the invariant mass (i.e., invariant mass is both conserved and invariant).

The mass-free energy equivalence formula gives a dissimilar prediction in non-isolated systems, since if energy is allowed to escape a system, both relativistic mass and invariant mass will escape also. In this example, the mass-energy equivalence formula predicts that the modify in mass of a arrangement is associated with the change in its energy due to energy being added or subtracted: ${\displaystyle \Delta one thousand=\Delta E/c^{ii}.}$ This form involving changes was the form in which this famous equation was originally presented past Einstein. In this sense, mass changes in any system are explained just if the mass of the energy added or removed from the system, are taken into account.

The formula implies that bound systems have an invariant mass (balance mass for the system) less than the sum of their parts, if the binding energy has been allowed to escape the system later the system has been bound. This may happen by converting organisation potential energy into some other kind of active free energy, such as kinetic free energy or photons, which easily escape a bound system. The divergence in system masses, called a mass defect, is a measure out of the binding energy in bound systems – in other words, the free energy needed to interruption the system autonomously. The greater the mass defect, the larger the binding energy. The binding energy (which itself has mass) must exist released (equally lite or rut) when the parts combine to form the bound system, and this is the reason the mass of the jump system decreases when the free energy leaves the system.^[19] The total invariant mass is actually conserved, when the mass of the binding energy that has escaped, is taken into account.

General relativity [edit]

In full general relativity, the total invariant mass of photons in an expanding volume of infinite will subtract, due to the ruby shift of such an expansion. The conservation of both mass and energy therefore depends on diverse corrections made to energy in the theory, due to the irresolute gravitational potential energy of such systems.

Run across besides [edit]

• Accuse conservation
• Conservation law
• Fick's laws of diffusion
• Constabulary of definite proportions
• Law of multiple proportions

References [edit]

1. ^ Volkenstein, Mikhail 5. (2009). Entropy and Information (illustrated ed.). Springer Science & Business concern Media. p. 20. ISBN978-3-0346-0078-one. Extract of folio 20
2. ^ Okuň, Lev Borisovič (2009). Energy and Mass in Relativity Theory. World Scientific. p. 253. ISBN978-981-281-412-8. Excerpt of page 253
3. ^ Lewis, David (2012). Early Russian Organic Chemists and Their Legacy (illustrated ed.). Springer Science & Business concern Media. p. 29. ISBN978-3-642-28219-5. Extract of page 29
4. ^ Mahavira is dated 598 BC - 526 BC. Come across. Dundas, Paul; John Hinnels ed. (2002). The Jains. London: Routledge. ISBN978-0-415-26606-two. p. 24
5. ^ Devendra (Muni.), T. G. Kalghatgi, T. Southward. Devadoss (1983) A source-book in Jaina philosophy Udaipur:Sri Tarak Guru Jain Gran. p.57. Also run into Tattvarthasutra verses 5.29 and 5.37
6. ^ Fr. 12; see pp.291–2 of Kirk, G. Due south.; J. Eastward. Raven; Malcolm Schofield (1983). The Presocratic Philosophers (2 ed.). Cambridge: Cambridge Academy Press. ISBN978-0-521-27455-v.
7. ^ Long, A. A.; D. N. Sedley (1987). "Epicureanism: The principals of conservation". The Hellenistic Philosophers. Vol 1: Translations of the master sources with philosophical commentary. Cambridge: Cambridge University Printing. pp. 25–26. ISBN978-0-521-27556-ix.
8. ^ Whitaker, Robert D. (1975-10-01). "An historical annotation on the conservation of mass". Periodical of Chemical Education. 52 (10): 658. Bibcode:1975JChEd..52..658W. doi:ten.1021/ed052p658. ISSN 0021-9584.
9. ^ Robert D. Whitaker, "An Historical Annotation on the Conservation of Mass", Journal of Chemical Pedagogy, 52, 10, 658-659, Oct 75
10. ^ Pismen, Len (2018). The Swings of Science: From Complexity to Simplicity and Back. Springer. p. 41. ISBN978-three-319-99777-3.
11. ^ Pomper, Philip (Oct 1962). "Lomonosov and the Discovery of the Law of the Conservation of Thing in Chemic Transformations". Ambix. 10 (iii): 119–127. doi:10.1179/amb.1962.10.3.119.
12. ^ Lomonosov, Mikhail Vasil'evich (1970). Mikhail Vasil'evich Lomonosov on the Corpuscular Theory. Henry G. Leicester (trans.). Cambridge, Mass.: Harvard University Printing. Introduction, p. 25.
13. ^ Дорфман, Яков (1961). Закон сохранения массы при химических реакциях и физические воззрения Ломоносова // Ломоносов М.В. Сборник статей и материалов, T.5. http://gidropraktikum.narod.ru/Lomonosov-Dorfman.djvu: М.-Л.: Издательство АН СССР. p. 193.
14. ^ Matthew Moncrieff Pattison Muir, The Elements of Chemistry (1904)
15. ^ Nouv. Recherches sur les lois des proportions chimiques (1865) 152, 171, 189
16. ^ "Conservation of Mass in Chemical Changes"Journal - Chemical Society, London, Vol.64, Part 2 Chemical Society (Great Uk)
17. ^ William Edwards Henderson, A Course in General Chemical science (1921)
18. ^ Ida Freund, The study of Chemic Composition: an account of its method and historical development, with illustrative quotations (1904)
19. ^ Kenneth R. Lang, Astrophysical Formulae, Springer (1999), ISBN 3-540-29692-1

yaliheavow.blogspot.com

Source: https://en.wikipedia.org/wiki/Conservation_of_mass

Share this post